Author Archives: Emily Barnard

Review Problems from Textbook

Posted on by
  • Supplemental Text on Difference Equation (you can find this on WebAssign)
    • Section 10.2: 3, 5, 7, 17
    • Section 10.3: Practice problem number 3, Exercises: 21, 27
    • Section 10.4: Exercises: 5 ,7, 9, 11

The remaining problems come from your textbook:

  • Section 1.4 (Limits) Exercises: 1-5 odds, 17-19 odds (try graphing these!)
  • Section 1.5 (Limits, continuity and differentiability)
    • See Figure 1 for helpful examples
    • Example 3 has many helpful figures
    • Exercises: 1-5 odds,
  • Section 1.6 (Practice with derivatives)
    • Exercises 1-33 odds, 39-43 odds
  • Section 1.8 (See also WebAssign Homework: Derivatives II and Applications of Derivatives)
    • Examples 3 and 4 we covered a similar examples in lecture
    • Exercises 7, 12 (Answers: (a) At point A; (b) negative; (c) It is zero; (d) backward; (e) It is back at the starting place and at rest; (f) The velocity is zero), 13, 15, 17, 18 (Answers: (a) picture b; (b) picture c; (c) picture d; (d) picture a; (e) Picture e.)
  • Section 2.1 (Graph sketching)
    • Exercises: 1,3, 13, 15 (For 13 and 15 try sketching in tangent lines to help you see how the slope is changing as you read from left to right.), 33
  • Section 2.2 (Graph sketching continued...)
    • Exercises: 7-17 odd, 23 (I suggest talking this one through with a neighbor)
  • Section 2.3 (Graph sketching continued...)
    • Exercises: 1-7 odd, 25-31 odd, 41
  • Section 2.5 (Optimization)
    • All three examples in this section are worth reviewing!
    • Exercises: 11, 13, 15, 17, 19 (For number 13: girth = perimeter of the square end.)
  • Section 3.1 (Practice with derivatives, product rule)
    • Exercises: 1-27 odds
  • Section 3.2 (Practice with derivatives, chain rule)
    • Exercises: 5-9 odds, 29-35
  • Section 4.2 (Exponential Function)
    • Exercises: 25-35 odds, 39, 41, 43
  • Section 4.3 (Exponential Function continued)
    • Exercises: 1-25 odd, Differential equations: 41, 43
  • Section 4.4 (The natural logarithm)
    • Exercises: 7-17 odd
  • Section 4.5 (The derivative of the natural logarithm)
    • Exercises: 1-19 odd
  • Section 4.5 (Using the laws of logarithms)
    • Exercises: 33-37 odd
  • Section 5.1 (Exponential growth and decay)
    • Exercises: 1, 5, 7, 13, 15, 17
    • WebAssign Assignment Applications: Exponential, Logarithmic Functions also has many good problems.
  • Section 6.1 (Indefinite integration)
    • Exercises: 1-45 odd, 55
  • Section 9.1 (Integration using substitution)
    • Exercises: 1-33 odd
  • Section 6.2 (Definite integration)
    • Exercises: 1-13 odd, 31, 33
  • Section 6.3 (Area under a curve)
    • Exercises: 19-23 odd, 33, 35
  • Section 6.4 (Area bounded between the curve and x-axis)
    • Examples 1, 2, and 9 are all worth reviewing
    • Exercises: 7-11 odd, 45
  • Section 6.5 (Applications of the definite integral)
    • Exercises: 1-9 odd, 29-35 odd (Average value and solids of rotation!)
  • Section 9.6 (Improper Integration)
    • Examples 1,2, 3 are all worth reviewing
    • Exercises: 13, 21-27 odd

Final Exam Broad Topics

Posted on by

In class we discussed about 12 of the most important topics from the course. You can find that list below. Consult the Unit Test Review Posts to find specific sections from your text book. As always, you're welcome to email me with your questions!

  • Difference Equations
    • Give the general solution; solve a word problem algebraically
    • Describe the graph of a difference equation
      • Increasing/Decreasing, Monotonic, Oscillating, Unbounded, Bounded (Your text uses the phrase "Asymptotic to a line" when the graph of a difference equation is bounded.)
      • You should be able to solve a difference equation using the graph of its solution
  • Limits
    • You should be able to draw the graph of a function satisfying 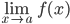 does not exist, for some number .
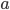    • You should be able to draw the graph of a function that is not continuous at a point.
    • You should be able to draw the graph of a function that not differential at a point.
  • Derivatives as a rate of change in applications
    • Applications involving a position function 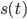(like a ball thrown straight up in the air, or a car traveling in a straight line).
      • The derivative is the (instantaneous) velocity.
    • Applications involving a population function 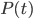, where 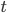is time.
      • The derivative is the growth rate of the population.
    • You should be able to use the tangent line at a point to predict position/population at a different time.
  • Derivative as slope of the tangent line
    • You should be able to use a graph of 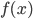and 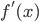to write the equation of a tangent line at a point
    • You should know:
      • If the derivative of 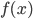is positive a point then 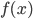is increasing near that point.
      • If the derivative of 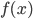is negative a point then 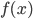is decreasing near that point.
  • Second Derivative as a rate of change of the first derivative
    • If the second derivative 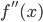is positive at a point, then the first derivative 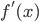is increasing near that point.
    • If the second derivative 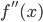is negative at a point, then the first derivative 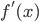is decreasing near that point.
    • You should know the physical physical interpretation of the second derivative as acceleration.
      • Good exercise: Given three graphs, can you determine which one is 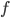, , 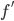and 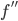? (See figures 21 and 23 from Section 2.2,  41, 42 from Section 2.3, and 31 and 31 from Section 2.4.)
  • Graph Sketching!
    • You should be able to...
      • Determine intervals of increasing and decreasing
      • Determine relative minima and maxima
      • Determine intervals of concavity
      • Determine inflection points
  • Optimization
    • Remember the difference between absolute maxima/minima and relative maxima/minima
  • Mechanics of taking derivatives
    • Including: Power rule, Product Rule and the Chain rule
  • Exponential and Logarithmic Functions
    • You should be able to interpret application problems dealing with:
      • Population growth
      • Radioactive decay
      • Carbon dating
  • Differential Equations and Slope-Fields
    • You should be able to sketch the slope-field for a given derivative.
    • You should be able to solve a differential equation of the form 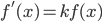. (Remember these are always of the form: .)
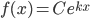  • Mechanics of Antidifferentiation
    • Including computing: indefinite integrals and definite integrals, and using substitution.
    • You should know the relationship between 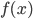and its antiderivative 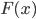. That is, .
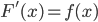  • Geometric Interpretation for the integral
    • When 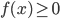this is the area under the graph of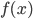
    • You should be able to compute Riemann Sums with left or right endpoints.
    • You should be able compute the area of the region bounded between the graph of a curve and the -axis.
      • Remember: This last problem involves finding out when a function is positive and when it is negative.
  • Applications of the integration
    • Average value of a function as a definite integral (Section 6.5)
    • Improper Integration and Infinite sums (Section 9.6)
    • Computing the distance versus displacement of an object in motion, given its velocity (Section 6.4)
    • Find the volume a solid of rotation (Section 6.5)