Difference equation material can be found in sections 10.1-10.4 of the supplemental text. You can find the supplemental text in the resources section of WebAssign, but I am also posting it here: ma_131_supplement
You should be able to:
- Write the difference equation for a word problem (applications in both finance and population growth). Sec. 10.1
- Write the general solution. (Don't forget about the special situation when
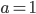 .) Sec. 10.2
.) Sec. 10.2 - Sketch the graph of various difference equations. Sec. 10.3
- Describe the long term behavior and vertical direction of the graph of a difference equation. Sec. 10.3
- Sketch the graph of a function that is:
- monotonic, oscillating, increasing, decreasing, constant, unbounded, bounded (asymptotic to a line).
- Sketch the graph of a function that is neither monotonic, oscillating, nor constant.
- Sketch the graph of a function that is:
- Solve a word problem by using the graph of the difference equation (see for example example 10 on page 400 of the supplemental text). Sec. 10.3
- Practice problem 3 may also be helpful (its solution is given after the homework problems). For the this type of problem, I would like you to include three graphs on your test.
- Solve a word problem using the general solution. Sec. 10.4
- You may be asked to solve for an initial deposit or loan amount; or a monthly withdrawal, payment or deposit amount.
You are also responsible for Sections 1.1-1.4 (pages 86-87 on the limit definition of the derivative) from the text book.
You should be able to
- Graph a linear equation and give its slope. Sec 1.1
- You should be able to use the power rule to compute the derivative of function at a point or as a function. Sec 1.2
- You should be able to give the slope of the tangent line for a function at a point
 either using the power rule or the graph of
either using the power rule or the graph of 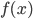 and
and 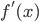 . See for example, Quiz 2. Sec 1.3
. See for example, Quiz 2. Sec 1.3 - You should be able to sketch the graph of a tangent line (as we did for
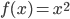 ).
). - You should be able to use the limit definition of the derivative to compute the derivative of a function
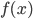 at a point
at a point  . See for example Example 7 from Section 1.3 and Examples 5-7 from Section 1.4. Sec 1.3-1.4
. See for example Example 7 from Section 1.3 and Examples 5-7 from Section 1.4. Sec 1.3-1.4
- I will provide the equation for this limit
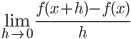 .
.
- I will provide the equation for this limit

