Test 1 Topics

Posted on by

Difference equation material can be found in sections 10.1-10.4 of the supplemental text. You can find the supplemental text in the resources section of WebAssign, but I am also posting it here: ma_131_supplement

You should be able to:

  • Write the difference equation for a word problem (applications in both finance and population growth). Sec. 10.1
  • Write the general solution. (Don't forget about the special situation when 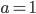.) Sec. 10.2
  • Sketch the graph of various difference equations. Sec. 10.3
  • Describe the long term behavior and vertical direction of the graph of a difference equation. Sec. 10.3
    • Sketch the graph of a function that is:
      • monotonic, oscillating, increasing, decreasing, constant, unbounded, bounded (asymptotic to a line).
    • Sketch the graph of a function that is neither monotonic, oscillating, nor constant.
  • Solve a word problem by using the graph of the difference equation (see for example example 10 on page 400 of the supplemental text). Sec. 10.3
    • Practice problem 3 may also be helpful (its solution is given after the homework problems). For the this type of problem, I would like you to include three graphs on your test.
  • Solve a word problem using the general solution. Sec. 10.4
    • You may be asked to solve for an initial deposit or loan amount; or a monthly withdrawal, payment or deposit amount.

You are also responsible for Sections 1.1-1.4 (pages 86-87 on the limit definition of the derivative) from the text book.

You should be able to

  • Graph a linear equation and give its slope. Sec 1.1
  • You should be able to use the power rule to compute the derivative of function at a point or as a function. Sec 1.2
  • You should be able to give the slope of the tangent line for a function at a point either using the power rule or the graph of 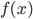and 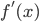. See for example, Quiz 2. Sec 1.3 
  • You should be able to sketch the graph of a tangent line (as we did for ).
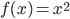  • You should be able to use the limit definition of the derivative to compute the derivative of a function 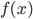at a point . See for example Example 7 from Section 1.3 and Examples 5-7 from Section 1.4. Sec 1.3-1.4 
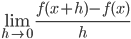    • I will provide the equation for this limit .